La (no) estructura de los números primos

Si hay un tema que ha fascinado a matemáticos y no matemáticos durante siglos son los números primos. Cuando era pequeño siempre me preguntaba por qué usaban esa relación de parentesco con esos números (¿primos de quién?), hasta que ya de adulto comprendí que primo era sinónimo de primario.

Y es que los números primos son para el conjunto de números enteros $\mathbb Z$ como los colores primarios son al arco iris; o como los sabores primarios son a la gastronomía. Son también como los elementos de la tabla periódica: todo lo que podemos tocar, ver u oler está hecho combinando adecuadamente esas piezas básicas.

En efecto, los números primos son los ladrillos indivisibles (átomos) que permiten construir todos los demás; multiplicativamente hablando, claro está. Desde el punto de vista de la suma, el asunto es trivial: todos los número nacen a partir del uno. En terminología de teoría de grupos podemos decir que los números primos son un sistema generador de $(\mathbb Z, \cdot)$.

Mucho se ha investigado acerca de qué comportamiento tiene la aparición de estos números dentro de $\mathbb Z$, pero poco se ha descubierto. La aparición de números primos aparenta tener un comportamiento caótico, y aunque se han encontrado ciertas "regularidades", queda mucho por conocer. Es quizá uno de las cuestiones matemáticas fáciles de formular (no hace falta ser un genio para entender el problema) que siguen sin ser resueltas.

Entendamos bien la cuestión. Los número pares, por ejemplo, tienen un comportamiento muy previsible: uno sí uno no. Si hablamos de los múltiplos de 6, sabemos que hay mucha regularidad, pues cada 6 números enteros hallamos uno de la familia.  Conjuntos de números más complicados, como los cuadrados perfectos, pueden ser descritos con alguna fórmula, como $n=k^2, k\in \mathbb Z$ en ese caso. Por muy rebuscado que busquemos la colección de números en cuestión, siempre se encuentra un método para describirla, así que, ¿cómo es posible que para un conjunto tan importante como el de números primos no tengamos casi nada?

La cuestión no es sólo mera curiosidad, que también (esa y no otra suele ser la principal motivación del matemático puro). El comportamiento de los números primos juega un papel crucial en la Criptología o teoría del cifrado de información, tan importante en el mundo de las transacciones digitales, las comunicaciones militares o la televisión de pago. Pues bien, a pesar de la presión económica que existe sobre el tema, los número primos siguen aguantando el tirón, ocultando su tan bien guardado secreto.

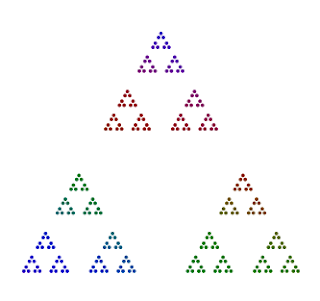
A la hora de descifrar el misterio de los números primos, además de técnicas de matemáticas avanzadas, como la función "zeta" de Rienman ζ(s), se han intentado muchos trucos visuales como la espiral de Ulam. El último que he conocido, y que me ha motivado a escribir esta entrada, es este de aquí:

http://www.datapointed.net/visualizations/math/factorization/animated-diagrams/

Es impresionante ver cómo aparecen los números primos (círculos perfectos) cuando menos te lo esperas. Pero no menos sorprendente es que podamos distinguir de un simple vistazo los números que son potencias de dos, o potencias de tres, o de cinco. O la estructura tan parecida que tienen el 243 y el 162, debido a que ambos tienen "en su interior" a $3^4$ (ojo, $243=3^4 \cdot 3$ y $162=3^4 \cdot 2$).

243

162

Asimismo es llamativo que los números que nos parecen raros tienen un "aspecto circular", apenas tienen estructura interna (por ejemplo el 183). En cambio, los "números redondos" tienen mucho nivel de organización interna (mirad el 200).

183

200

En definitiva, estos diagramas no revelan el misterio de los números primos pero proporcionan un pequeño avance, pues creo que la visualización es el germen de cualquier buena idea matemática.